Informatyka

Temat: Algorytmy w praktyce

Czym jest programowanie?

Programowanie to umiejętność rozmowy z komputerem. Rozmawiamy z komputerem w zrozumiałych dla niego językach, czyli językach programowania. Dajemy komputerowi polecenia, co ma zrobić, a on w odpowiedzi pokazuje nam wyniki swojej pracy. Osobę, która programuje, nazywamy programistą lub developerem.

Algorytmy – skończony ciąg jasno zdefiniowanych czynności koniecznych do wykonania pewnego rodzaju zadań, sposób postępowania prowadzący do rozwiązania problemu. Można go przedstawić na schemacie blokowym.

Zadaniem algorytmu jest przeprowadzenie systemu z pewnego stanu początkowego do pożądanego stanu końcowego. Badaniem algorytmów zajmuje się algorytmika. Algorytm może zostać zaimplementowany w postaci programu komputerowego.
Jako przykład stosowanego w życiu codziennym algorytmu podaje się często przepis kulinarny. Dla przykładu, aby ugotować bigos, należy w określonej kolejności oraz odstępach czasowych (imperatyw czasowy) dodawać właściwe rodzaje kapusty i innych składników. Może istnieć kilka różnych przepisów dających na końcu bardzo podobną potrawę. Algorytmy zwykle formułowane są w sposób ścisły w oparciu o język matematyki.
                    
Algorytm Euklidesa - służy do obliczania NWD (największego wspólnego dzielnika) dwóch liczb całkowitych.

NWD - Euklides dzielenie liczb

Algorytm do obliczenia NWD(a,b), wykonujemy kolejno następujące kroki:

Dzielimy z resztą liczbę a przez liczbę b
1. jeżeli reszta jest równa 0, to NWD(a,b)=b
2. jeżeli reszta jest różna od 0, to przypisujemy liczbie a wartość liczby b, liczbie b wartość otrzymanej reszty, a następnie wykonujemy ponownie punkt 1.

Przykład 1. Wyznacz największy wspólny dzielnik liczb 282 i 78.

Rozwiązanie:

Zaczynamy od podzielenia liczby 282 przez liczbę 78 z resztą:

      282 : 78 = 3, reszty 48

Otrzymaliśmy resztę różną od zera, zatem teraz podzielimy liczbę 78 przez resztę 48. Ten schemat będziemy powtarzać do momentu otrzymania reszty równej 0.

      78 : 48 = 1, reszty 30
      48 : 30 = 1, reszty 18
      30 : 18 = 1, reszty 12
      18 : 12 = 1, reszty 6
      12 :  6 = 2, reszty 0

Otrzymaliśmy resztę równą zero, zatem szukany NWD będzie równy ostatniej niezerowej reszcie:

      NWD(282, 78) = 6

NWD - Euklides odejmowanie liczb

Przykład 2

Wyznacz największy wspólny dzielnik liczby 21 i 18.

Odejmujemy liczby dopóki się nie zrównają od większej odejmujemy mniejszą:

      (21, 18) → (21-18, 18)
      (3, 18) → (3, 18-3)
      (3, 15) → (3, 15-3)
      (3, 12) → (3, 12-3)
      (3, 9) → (3, 9-3)
      (3, 6) → (3, 6-3)
      (3, 3) - koniec, NWD(21,18) = 3

      NWD(21, 18) = 3

Programowanie - krokowy Algorytm Euklidesa wyznaczania NWD dwóch liczb a i b

Wejście:

      a,b - liczby naturalne, których NWD oblicza algorytm

Wyjście:

      a lub b - wartość NWD pierwotnych liczb a i b.

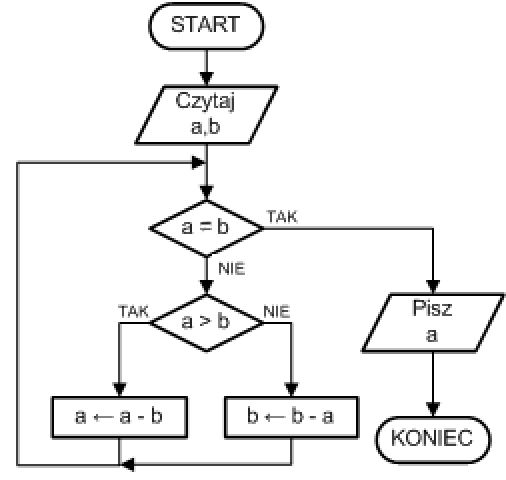
Krok 1: Czytaj a,b ; wczytujemy dane wejściowe
Krok 2: Jeśli a = b, to idź do kroku 5 ; jeśli a = b, to NWD jest a lub b
Krok 3: Jeśli a > b, to a ← a - b. Inaczej b ← b - a ; jeśli a jest różne od b, to od większej liczby odejmujemy mniejszą
Krok 4: Idź do kroku 2 ; wracamy do sprawdzania warunku w kroku 2
Krok 5: Pisz a ; wypisujemy NWD
Krok 6: Zakończ ; koniec algorytmu


Schemat blokowy



Powinieneś umieć: